|
基于时频域的钢桶泄漏检测信号处理(3)
范佩西
第三章 泄漏声发射信号的时频分析
本文是利用MATLAB软件对钢桶声发射信号进行仿真时频分析处理。根据采集到的钢桶声发射数据设波形的采样频率fs为1000kHz,采样点数N为2048个,则时间t=n/fs,n为2048个点中的任意一点,n=0:N-1。分别在声发射信号的时域和频域对信号进行分析。
3.1 泄漏信号的频域分析
钢桶泄漏声发射信号具有很宽的频谱,它不仅包括可听声波范围内的频率成分,而且还包括超声频段内的频率成分。这些频率成分的信号和噪声都可能沿着泄漏钢桶传播到传感器,所以传感器采集到的泄漏信号的频谱有比较丰富的成分[1]。如图3.2所示,有一定的泄漏信号存在于从0-150KHz频率范围内。而我们需要的对钢桶泄漏检测有用声发射信号的只是某一频段的信号,其他的不是我们所需要的,而且还对检测信号有影响,所以我们必须对采集到的声发射信号进行处理,需要除掉没有的部分,留下我们需要的部分。
3.1.1 频谱分析
傅里叶变换是一种分析信号的方法[2],它可分析信号的成分,也可用这些成分合成信号[2]。MATLAB中提供了多种实现快速变换的函数,如fft,ifft,fft2,ifft2等函数。其中fft2、ifft2是对离散数据分别进行二维快速傅里叶正、反变换。fft、ifft则是对离散数据分别进行一维快速傅里叶正、反变换[2]。由于MATLAB中没有零下标,因此,它采用的公式上、下标都相应右移一位。
下面对实验采集到的钢桶声发射信号做FFT,程序代码如图3.1所示。

图3.1 FFT部分程序代码
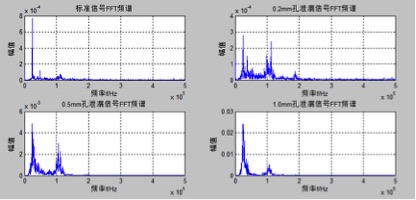
图3.2 钢桶声发射信号的频谱图
经FFT得出如图3.2所示的波形。比较泄漏信号与标准信号的FFT,泄漏信号在110KHz附近的幅度明显比标准信号的大。比较不同泄漏孔径大小的泄漏信号,110KHz附近的幅度随孔径的增大而增大。所以泄漏声发射信号的特征频率明显是在110kHz附近,而25kHz附近的为噪声频率。
3.1.2 泄漏声发射信号的降噪处理
钢桶泄漏声发射信号经过钢桶壁、传感器、信号采集卡、传输设备、放大器等会使信号伴随有很多噪声,这些噪声的大量参入使钢桶泄漏源的声发射信号发生改变,从而会使钢桶泄漏检测的精确性和准确度降低,所以我们必须寻找一定的信号处理方法来降低噪声,是真正的泄漏声发射信号强度增大。
由以上FFT得到的频谱图可知,钢桶泄漏声发射信号在频域内有两处比较明显的突起,一个为噪声,一个为声发射信号特征频率。因为钢桶声发射特征频率在110kHz附近,我们需要滤掉高频和低频的信号,又因为钢桶泄漏声发射信号是一类非平稳的随机信号,所以应该选择一种适合非平稳的随机信号的滤波方法——FIR带通滤波[26]。
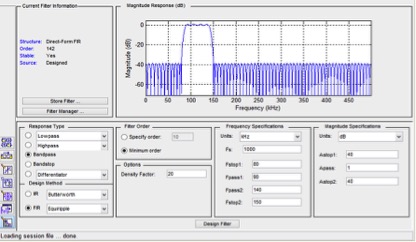
图3.3 FIR滤波器界面
文中主要采用MATLAB工具FDATool的设计FIR滤波器,如图3.3所示。可以有效的实现对声发射信号的滤波。基于钢桶泄漏声发射信号特征和FIR滤波器各具体参数要求[23],初步设计得到滤波器幅值—频率图如图3.4所示,和相位延迟图如图3.5所示,其主要滤波器参数设置为:(1)响应类型为带通;(2)设计方法为等波纹;(3)滤波阶数为最小阶数;(4)密度因素为20;(5)频率参数中采样频率Fs=1000kHz,带通频率Fpass1=90kHz, Fpass2=140kHz,带阻频率Fstop1=80kHz,Fstop2=150kHz通带纹波Apass=1dB,阻带衰减Astop1=40dB,Astop2=40dB。
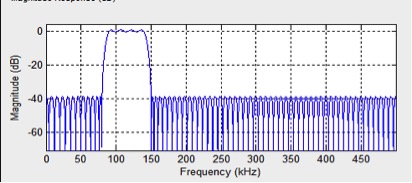
图3.4 幅值—频率图
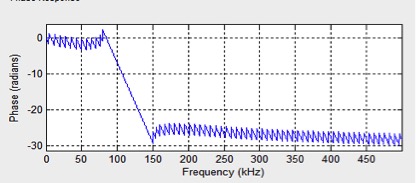
图3.5 相位延迟图
利用设计好的滤波器对采集到的钢桶声发射信号进行滤波,步骤如下:打开fdatool界面的file,选择Export;输出的变量名默认为Num,然后在编辑器里设置b=Num,a=1,x=filter(b,a,A);具体程序如图3.6所示。经过滤波器滤波后得到钢桶声发射信号波形如图3.7所示。

图3.6 滤波程序部分代码
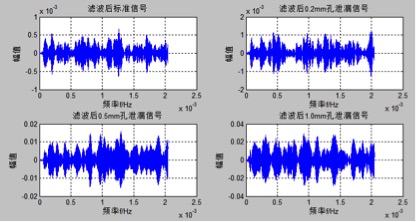
图3.7 滤波后声发射信号时域波形
在时域中比较声发射滤波前后如图3.15和图3.7,可见图3.7中的低频噪声经过滤波器滤波后得到了弱化,这样使得滤波后的时域信号波形比原信号的波形更加清晰可见,如图可知,滤波后的信号中还存在一些低频干扰,使滤波后时域信号出现高低不定的不规则脉冲。而且在对声发射信号滤波的开始时还出现了小部分信号的失真,这失真主要是因为滤波器在进入完全工作前的延迟所致[4]。
3.1.3 功率谱估计
功率谱估计的目的是根据有限数据给出信号、随机过程的频率成分分布描述。对滤波后的钢桶声发射信号进行功率谱估计得到如图3.9所示波形。具体程序如图3.8所示:

图3.8 功率谱估计部分程序代码
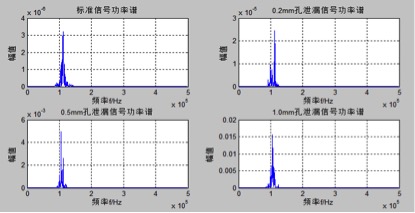
图3.9 声发射信号功率谱密度
根据对多组采集到的钢桶声发射信号进行功率谱估计分析可知,声发射功率谱密度幅值是随钢桶的泄漏孔径增大而增大的,而标准钢桶的声发射信号的功率谱密度最大幅值在310-6左右。若钢桶的声发射信号的功率谱密度最大值的数量级超过了110-5则该钢桶很可能为泄漏钢桶。
3.1.4希尔伯特黄变换(HHT)
希尔伯特黄变换通过对声发射信号局部特征分析,由信号本身的构造基函数分析,分解获得不同大小的声发射信号分量。本证模态函数代表了钢桶声发射信号的内在波动模式,对经验模态分解后的固有模态函数分量进行分析可获取信号中比较丰富的丰富的时频能量信号,如图10所示,对采集到的0.5mm孔径泄漏状态下的声发射信号进行经验模态分解,分解图形如图3.11所示,并对分解后的信号进行希尔伯特谱分析和边际谱分析。

图3.10 经验模态分解部分程序代码
从图3.11中可以看出,经过经验模态分解获得了7个固有模态函数分量,经过对这几个分量的具体分析可知,第1个固有模态函数分量为钢桶泄漏声发射信号中的特征频率最大的分量,它对应的是频率为110kHz左右的泄漏声发射信号,而第2个固有模态函数分量对应的是频率为25kHz的噪声信号,而第7个固有模态函数分量则为钢桶泄漏声发射信号中的特征频率最小的分量。
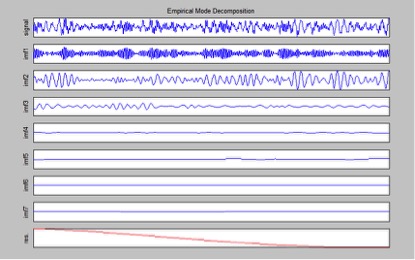
图3.11 泄漏信号的经验模态分解图
我们对图3.11中的泄漏信号经过经验模态分解所得到的固有模态函数分量进行希尔伯特变换,可以得到的如图3.12所示的希尔伯特谱和如图3.13所示的边际谱。在图3.12中和图3.13中有位于25kHz附近和位于110kHz附近的信号频率,在根据前面分析的频谱和功率谱可知,25kHz附近的信号为噪声,而钢桶泄漏声发射信号的频率位于110kHz附近。分别对不同大小孔径的钢桶声发射信号做希尔伯特黄变换得出信号的能量变化,泄漏孔径越大,边际谱的能量就越大。
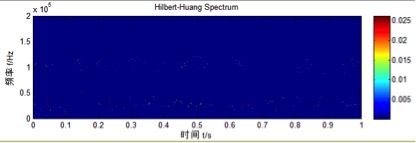
图3.12 泄漏信号希尔伯特谱图
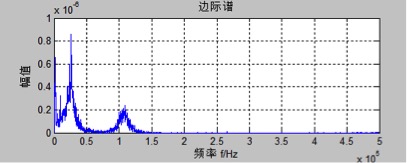
图3.13 泄漏信号边际谱图
分别对滤波后的多组标准钢桶声发射信号数据和不同泄露孔径大小的钢桶声发射信号数据进行边际谱分析比较,得出标准钢桶声发射信号的边际谱最大值都低于1.3,若钢桶的声发射信号的边际谱超过了1.3,则该钢桶为泄漏钢桶。
3.2 泄漏信号的时域分析
3.2.1 信号的时域仿真波形及其分布
从声发射信号的时域波形上可以看到钢桶泄漏信号的幅值特征随钢桶泄漏孔径变化的变化随时间变化情况的反映,因此,从时域仿真波形中可以看出幅值的变化。在钢桶泄漏实际检测过程中,由于钢桶泄漏源声发射信号很微弱,通常利用放大电路对采集到的微弱泄漏声发射信号进行放大,转化为一定大小的数字信号数据,然后再经输入设备输入计算机进行分析处理。如图3.14所示,将标准信号、0.2mm孔径泄漏信号、0.5mm孔径泄漏信号、1.0mm孔径泄漏信号的数据分别赋给A B C D,然后进行绘图,横坐标为时间,纵坐标为幅值,运行程序。运行结果如图3.15所示。
如图3.15所示,钢桶泄漏声发射信号的仿真时域波形上只能得到声发射泄漏信号幅值的大概变化,而不能对信号进行详细的描述和分析。因此要想获得钢桶泄漏声发射信号的时域特征参数,我们还需要对声发射信号做进一步的定量分析。

图3.14 绘制时域波形程序
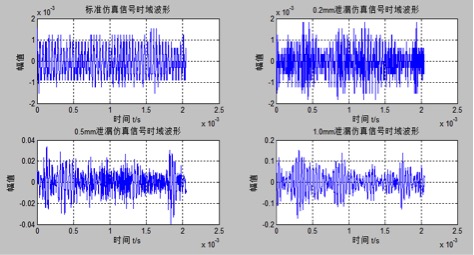
图3.15 钢桶声发射信号时域波形
为了更好的分析钢桶泄漏声发射信号的时域特征参数的特点,将输入到计算机的钢桶泄漏声发射信号分别按照标准钢桶声发射信号和泄漏钢桶泄漏时孔径大小不同的声发射信号分成5组,分别对每一组信号的幅值进行统计,根据统计结果做出表格,由表格来分析信号幅值的特征。
表3.1 泄漏孔径大小与幅值的关系
| 孔径大小 |
0mm(标准) |
0.2mm |
0.3mm |
0.5mm |
1.0mm |
幅值大小v |
0.0012 |
0.0019 |
0.0067 |
0.025 |
0.14 |
由表3.1可以看出,在钢桶内压力大小相同时,泄漏的孔径越大,声发射信号的幅值就越大。
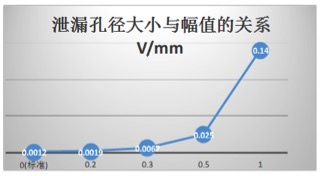
图3.16 泄漏孔径大小与幅值的关系
依次将表3.1的上的点的坐标连接起来,则可画出标准钢桶和不同泄漏孔径钢桶泄漏信号的幅值分布曲线,如图3.16。从图中可以看出钢桶泄漏声发射信号随声发射源特征不同而不同的幅值分布。其分布是有标准钢桶和随钢桶桶泄漏孔大小的不同而不同的,当泄漏孔直径较大时,钢桶声发射信号幅值较分散,它的正负幅值的最大差就越大,当钢桶泄漏孔直径较小或不泄露时,钢桶声发射信号的幅值则更集中,它的正负幅值的最大就越小。这说明泄漏信号的分布与泄漏孔径有很大的关系。
3.2.2 声发射时域信号的均值(SAL)及均方值(RMS)
对随机信号时域特征参数的分析是有效描述随机信号的方法,声发射信号的时域特征参数主要有均方值、均值和方差等。分别对标准钢桶、0.2mm、0.5mm、1.0mm孔径大小的泄漏钢桶做实验,每组作五次,程序如图3.17所示。如表3.2所示,分别求出几组滤波后钢桶声发射信号的均方值和均值。

图3.17 求均值均方值部分程序
表3.2 泄漏信号时域特征量计算结果
| 孔径 |
特征量 |
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
标准(0mm) |
均值 |
-8.5027e-07 |
-6.79274e-07 |
-5.70537e-07 |
-9.55546e-07 |
-8.18635e-07 |
均方值 |
0.00017607 |
0.000206035 |
0.000160567 |
0.000169151 |
0.000164451 |
0.2mm |
均值 |
-1.0008e-06 |
-9.33033e-07 |
-9.51477e-08 |
-8.98199e-07 |
-6.04869e-07 |
均方值 |
0.00037687 |
0.000381093 |
0.00035149 |
0.000352732 |
0.000373246 |
0.5mm |
均值 |
5.9555e-08 |
2.53018e-06 |
-2.5355e-06 |
5.61606e-07 |
-5.76241e-06 |
均方值 |
0.00511135 |
0.00518833 |
0.00524539 |
0.00611025 |
0.00552995 |
1.0mm |
均值 |
-1.2324e-05 |
1.15988e-06 |
4.02003e-06 |
-1.02038e05 |
4.22021e-06 |
均方值 |
0.0106125 |
0.0118906 |
0.0118194 |
0.00949618 |
0.0111874 |
从表3.2中可知,均值的不能显示出钢桶泄漏源的特征。而对于均方值,在相同泄漏孔径大小的钢桶泄漏信号的均方值每次测试的结果变化不大;而不同孔径的钢桶的均值是随着孔径的变大而变大。由此可见,在工程中可以由均方值的大小来判断泄漏孔的大小。
3.3本章小结
本章详细叙述了泄漏信号的特点及处理方法,分别对泄漏信号的时域和频域进行研究,重点对泄漏信号的时域均方值、快速傅里叶变换、功率谱、希尔伯特黄变换进行了实验研究和分析。运行自己开发的钢桶泄漏声发射信号检测系统对钢桶声发射信号进行分析处理,得出滤波后钢桶泄漏信号的分析结果如下表所示:
表3.3 不同泄漏孔径的信号特征参数
| 泄漏孔径大小 |
均方值(RMS) |
FFT最大幅值 |
功率谱最大幅值 |
边际谱最大幅值 |
标准(0mm) |
0.000176075 |
0.00010011 |
5.1312e-06 |
9.6792e-09 |
0.2mm |
0.000386193 |
0.00021886 |
2.4524e-05 |
2.24584e-08 |
0.5mm |
0.00511135 |
0.0031134 |
0.004963 |
4.8933e-07 |
1.0mm |
0.0106125 |
0.0055116 |
0.015553 |
8.8119e-07 |
根据表3.3得出,泄漏声发射信号的频域特征参数和均方值是随钢桶泄漏孔径的增大而增大。
[1] 姜涛.管道泄漏检测与定位的应用研究[D].哈尔滨工程大学,2008.
[2] 杨丽娟,张白桦,叶旭桢.快速傅里叶变换FFT及其应用[J].光电工程,2004,31(增刊):1-7.
[3] 胡丽莹,肖蓬.快速傅里叶变换在频谱分析中的应用[J].福建师范大学学报(自然科学版), 2011(04).
[4] 宋爱国,刘文波等.测试信号分析与处理[M].机械工业出版社,2007.
[5] 黄振峰,伍蒋军,毛汉领.金属裂纹声发射信号FIR滤波设计的滤波器参数设置方法[J].河北工业大学学报,2007(01):36.
[6] 于浩.石油管线泄漏的声发射技术(AE)监测系统研究[D].西安科技大学,2009.
【相关链接】
基于时频域的钢桶泄漏检测信号处理(1)
基于时频域的钢桶泄漏检测信号处理(2)
基于时频域的钢桶泄漏检测信号处理(3)
基于时频域的钢桶泄漏检测信号处理(4)
基于时频域的钢桶泄漏检测信号处理(5)
|

