《包装设计制作工艺与检测技术标准实用手册》

第四篇　包装设计基础

第三章　包装容器结构设计

第一节　纸包装容器结构设计

2．管式折叠纸盒的旋转性、成型角和旋转角

（1）旋转性。管式折叠纸盒盒体的成型过程，可以看成是与盒底面截交的各个侧面，以相邻两侧面的相交线为轴，依次旋转一定角度而成型。见图4－3－22，正四棱柱纸盒和正六棱柱纸盒，其侧面B′BCC′面、C′CDD′面……分别以BB′、CC′……为轴依次旋转90°和60°而成型。管式折叠纸盒这种连续旋转成型特性即为管式折叠纸盒的旋转性。

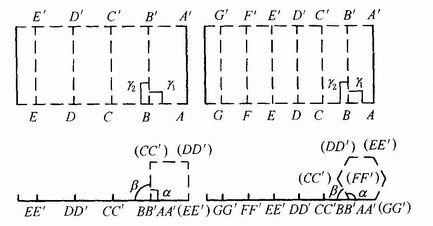
图4－3－22　管式折叠纸盒的旋转性

（2）成型角

A成型角　如图4－3－22所示，在成型时，相邻两侧的底边（或顶边）所构成的角，称为第一类成型角，简称A成型角，用α表示。

B成型角　在各个侧面中，底边（或顶边）与旋转轴（相邻两侧面的交线）所构成的角称为第二类成型角，简称B成型角，用γi表示（图4－3－22）。

（3）旋转角。在成型中，相邻两侧面的底边或顶边以其交点为轴，所旋转的角即为旋转角，用β表示（见图4－3－22）。在实际上，管式折叠纸盒盒底（或盒盖）在成型过程中，相邻两侧面的摇翼为构成A成型角而旋转的角度即等于β。

由于管式折叠纸盒是由一平面纸板折叠而成，故就同一旋转点来说，A、B类成型角和旋转角之间存在如下关系：

β＝360°－（α＋Σγi）　　　　（4－3－4）

式中　β———旋转角，（°）；　α———A成型角，（°）；∑γi———B成型角之和，（°）。

3．管式折叠纸盒的盒盖结构

对于纸盒盒盖的结构设计，首先应考虑便于被包装物的装入和取出，在被包装物装入后不会自开，起到保护被包装物的作用；其次盒盖应能易开和易封。

在盒盖的设计中，可采用以下几种方法固定盒盖，防止自开。

a．利用纸板间的摩擦作用，固定盒盖。

b．利用纸板上的卡口，卡住摇翼，固定盒盖。

c．利用插口插舌结构，将摇翼互相锁合，固定盒盖。

d．利用摇翼互相插撇锁合，固定盒盖。

e．利用粘合剂将摇翼粘合，固定盒盖。

管式折叠纸盒盒盖的种类很多，有具有多次开启功能的；有防伪和防盗功能，只能开启一次，不能复原的；有虽然只能开启一次，但在取出被包装物后可以在新的位置做新盖的；还有在开启后可以兼做广告板的。

盒盖的结构形式按盒盖固定方式的不同主要有如下几种。

（1）插入式。见图4－3－23，插入式盒盖在盒的端部设有3个摇翼，主摇翼适当延长，封盖时插入盒体。此种盒盖具有再封合功能，可多次使用。插入式盒盖有飞机式、反插式和直插式3种。

（2）锁口式。锁口式盒盖一般有4个摇翼，在相对的两个主摇翼上设计有相应的插口和插舌，见图4－3－24。这种结构是利用主摇翼上的插舌插入相应摇翼的插口内，固定盒盖。其特点是封合牢固，但开启稍嫌不便。

（3）插锁式。插锁式盒盖是插入式和锁口式相结合的一种盒盖结构。常见的两种结构见图4－3－25。

图4－3－23　插入折叠纸盒

a．飞机式；b．反插式；c．直插式

（4）连续摇翼窝进式。这是一种特殊的锁口形式，主要用于正多边形管式折叠纸盒的盒盖（或盒底）结构，见图4－3－26。其特点是封口比较牢固，可通过折叠组成造型优美的图案，但手工组装比较麻烦。一般用作礼品包装。

图4－3－24　锁口式折叠纸盒

图4－3－25　插锁式折叠纸盒

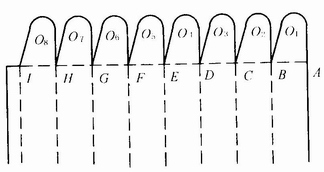
图4－3－26　正n方棱连续摇翼窝进式盒盖

连续摇翼窝进式盒盖的设计要点是寻找各摇翼折插后的相交点O。对该点的要求是它必须位于各摇翼的轮廓边线上或折痕线上，否则摇翼就无法折插并相互锁合。而对摇翼的形状，既可用简单明快的直线，也可采用复杂多变的曲线。

各摇翼相交点的确定主要有以下两种情况：

①正n边形。对于正n边形连续摇翼窝进式纸盒盒盖摇翼的相交点，在设计中一般选择其几何中心。见图4－3－27，正四边形盒盖的相交点位于其几何中心，也位于A成型角（∠BAD）的角平分线AO与顶边AB的中垂线OH的交点上。

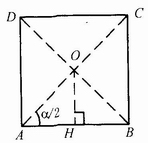
图4－3－27　正四边形盒盖成型图

对于正n边形，其A成型角计算公式为：

α＝［180°×（n－2）］／n　　　　（4－3－5a）

故：

α／2＝［180°×（n－2）］／2n　　　　（4－3－5b）

式中　α———A成型角，（°）；　n———正n边形的边数。

由以上分析可知，正n边形各摇翼相交点的确定方法为：通过摇翼侧面顶边的一个旋转点，作与顶边成α／2的射线和该顶边中垂线的交点，即确定了该摇翼相交点的位置。其它摇翼用与此相同的方法确定。

该方法同样适用于正n棱柱和正n棱台管式折叠纸盒盒盖的摇翼设计。

②任意n边形。确定任意n边形连续摇翼窝进式纸盒盒盖摇翼相交点的方法较多，有展开法、垂足法和旋转角法等。见图4－3－28，在此以任意三边形为例介绍展开法求解盒盖摇翼的相交点。

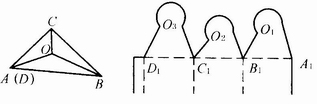
图4－3－28　任意三边形相交点的求法

求解盒盖各摇翼相交点Oi的步骤如下：

第一步，选取盒盖上的任意相交点O（见图4－3－28a），连接相交点O与旋转点的连线OA、OB、OC；

第二步，将三角形ABC依次展开成线段A1B1C1D1；

第三步，在线段A1B1上以A1点为圆心，以OA为半径作一圆弧，然后再以B1点为圆心，以OB为半径再作一圆弧，两圆弧相交点O1就是A1B1侧面摇翼上的相交点；

第四步，按第三步相同的方法求取B1C1，C1D1侧面摇翼上的相交点O2和O3。

以此类推对任意正n边形，均可采用上述展开法求取各摇翼上的相交点Oi。此外展开法还可用于求盒盖上各摇翼的重合点，以便在盒盖上打孔来安装缎带等物。

其它确定连续摇翼窝进式纸盒盒盖摇翼相交点的方法，由于篇幅所限在此不再赘述。

返回目录页