《包装设计制作工艺与检测技术标准实用手册》

第四篇　包装设计基础

第三章　包装容器结构设计

第一节　纸包装容器结构设计

3．盘式折叠纸盒的盒盖结构

（1）罩盖式。其盒盖盒体是两个独立的盘式结构，盒盖的长度和宽度尺寸一般比盒体略大些。这种纸盒多用于高度较小而盒面积较大的商品，便于展示装潢设计。

按照盒体盒盖的相对高度，罩盖盒可分为3种结构类型。

①天罩地式　H′1≥H1（图4－3－45a），盒盖完全罩住盒体。

②帽盖式　H′1＜H1（图4－3－45b），盒盖只罩住盒口部分。

③对口盖式　H＝H′1＋H1（图4－3－45c），盒盖罩住盒口的插口部分。

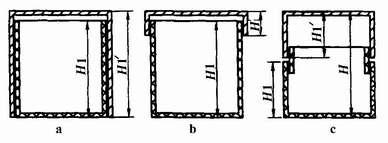
图4－3－45　罩盖盒的结构类型

对于罩盖盒，其有关尺寸计算公式为：

盒体　　　X＝Xi＋（m＋1）t＋kX　　　　（4－3－10）

　　　　　X0＝X＋t＝Xi＋nt＋kX　　　　（4－3－11）

盒盖　　　X′＝X0＋（m－1）t＋kX′＝Xi＋（m＋n－1）t＋kX＋kX′　　　　（4－3－12）

　　　　　X′0＝X1＋（m＋n）t＋kX＋kX′　　　　（4－3－13）

式中　Xi———盒体内部尺寸，mm；　X———盒体制造尺寸，mm；　X0———盒体外部尺寸，mm；　X′———盒盖制造尺寸，mm；　X′0———盒盖外部尺寸，mm；　n———盒体纸板层数；　m———盒盖纸板层数；　t———纸板厚度，mm；　kX———盒体制造尺寸修正函数，mm；　kX′———盒盖制造尺寸修正系数，mm。

（2）摇盖式。盘式摇盖盒是在盘式盒的基础上加以铰链式摇盖组成全封口结构的盘式盒。此类盘式纸盒有单摇盖和双摇盖两种，见图4－3－46。

图4－3－46　盘式摇盖纸盒
a．单摇盖纸盒；b．双摇盖纸盒

（3）插别式。此类盘式折叠纸盒类似于连续摇翼窝进式盒盖，见图4－3－47。

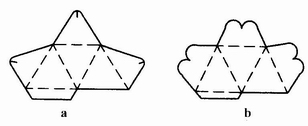
图4－3－47　插别式盘式折叠纸盒

（4）正掀封口式。正掀封口式盘式折叠纸盒的盒盖与管式折叠纸盒中的正掀封口式盒盖相同，见图4－3－48。

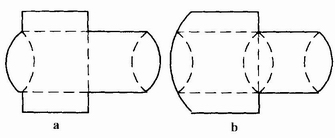
图4－3－48　正掀封口式盘式折叠纸盒

4．盘式自动折叠纸盒的结构设计

（1）盘式自动折叠纸盒。盘式自动折叠纸盒成型后，可将两端侧板折向盒内，而将整个纸盒折成平板状，使用时，只要张开盒身，纸盒就能自动恢复成型。

根据其折向有内折叠盘式纸盒和外折叠盘式纸盒，即纸盒左右的侧板折向盒内时，其前后侧板向外翻折时为外折叠盘式纸盒；而当纸盒的左右侧板折向盒内时，前后侧板也折向盒内的为内折叠纸盒，见图4－3－49。

最典型的盘式自动折叠纸盒是毕尔斯（Beers）式折叠纸盒和布莱特伍兹（Bright－woods）式折叠纸盒。它们最大的特点是γi＝90°。这两种盘式自动折叠纸盒结构见图4－3－50，均有内折叠式和外折叠式两种，结构样式大同小异。

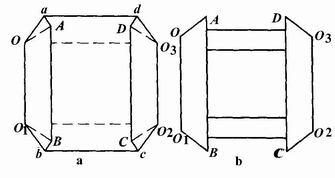
图4－3－49　盘式自动折叠纸盒折成平板状图
a．外折叠纸盒；b．内折叠纸盒

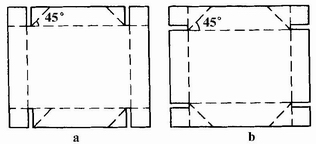
图4－3－50　毕尔斯式和布莱特伍兹式自动折叠纸盒
a．毕尔斯式；b．布莱特伍兹式

（2）内折叠角。设计盘式自动折叠纸盒时，一般先要计算其内折叠角的大小。内折叠角的含义为：为使棱台形盘式自动折叠纸盒在成型后，其两侧的侧板能向盒内平折，在侧板上形成的折叠线与纸盒底边构成的角见图4－3－51中的∠C1OO3（或∠COO3）。

内折叠角的一般计算公式为：

θ＝12（α＋γ1－γ2）　　　　（4－3－14）

式中　θ———盘式自动折叠纸盒的内折叠角，（°）；　α———A成型角，（°）；　γ1———内折叠角所在盒板即侧板的B成型角，（°）；　γ2———与γ1所在盒板即端板的B成型角，（°）。

（3）外折叠角。外折叠角的含义为：为使棱台形盘式自动折叠纸盒成型以后其两侧侧板能向盒外平折，在侧板上形成的折叠线与纸盒底边所构成的角，见图4－3－52中的∠COO3，用θ′表示。

外折叠角的一般计算公式为：

θ′＝（γ1＋γ2－α）／2　　　　（4－3－15）

式中　θ′———盘式自动折叠纸盒的外折叠角，（°）；　α———A成型角，（°）；　γ1———外折叠角所在盒板的B成型角，（°）；　γ2———与γ1相邻盒板即边板的B成型角，（°）。

对于前述的毕尔斯式和布莱特伍兹式盘式折叠纸盒，由于其α＝γ1＝γ2＝90°，此类纸盒的内折叠角和外折叠角相等均匀45°。

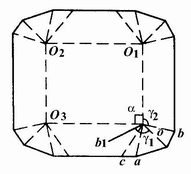
图4－3－51　盘式自动折叠纸盒内折叠角

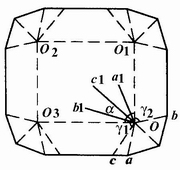
图4－3－52　盘式自动折叠纸盒外折叠角

返回目录页