《包装设计制作工艺与检测技术标准实用手册》

第二篇 包装技术与工艺

第二章　防潮（湿）包装技术

第二节　防潮包装原理

一、包装材料的透湿机理

除一定厚度以上的金属、玻璃、部分陶瓷材料不透湿外，对于大多数材料来说，都有一定的透湿性。以某种透湿材料为界限，隔开两侧空间，当两侧的空气湿度存在差别时，则高湿度一侧空气中的湿气（即水蒸气），就会通过材料，向低湿度一侧的空气中透过。材料的透湿程度是由材料的种类、内部结构、厚度以及环境温度及材料两侧水蒸气的压力差（或湿度差）决定的。金属箔、玻璃薄片、部分陶瓷的透湿，主要是由材料内部的空穴结构引起的毛细流动所造成的。纸、纸板、塑料板、塑料膜、橡胶制品、木板材料等的透湿，主要是由纤维或主分子链之间搭接程度疏密不均造成了许多微小的空隙，其中包括分子间空隙与分子内空隙，使活化的水分子扩散或迁移所造成的。所以说，包装用塑料薄膜的透湿现象主要是由活性水分子扩散而导致的。另外，吸湿性塑料因表面对水分子有较强的吸附能力，从而使水分子对材料的溶解能力增加，使得这种材料的透湿性能增强。

由于塑料薄膜用于防潮包装比较多，并且具有其他包装材料的共同特点，所以我们以塑料薄膜的透湿机理来研究包装的防潮原理。

二、透湿量及其计算公式

透湿量是指透过某一包装材料的水蒸气量（Q），单位用g表示。

假若将一厚度为L，表面积为A的薄膜，置于两侧分别为高湿度PH（水蒸气压力）（或hH（相对湿度））和低湿度PL（或hL）的空气中，高湿度一侧的薄膜表面就会吸附一定量湿气（水分子），被吸附的湿气就会进一步溶解到材料的分子结构中，其中具有活性的水分子会继续向材料内部扩散，最后达到材料的另一侧逸出并挥发到低湿度的空气中。这一过程需要延续一定时间后，才能达到透湿的稳定状态，即高湿侧材料表面水分子溶解进入的量与低湿侧材料表面水分子逸出的量相等的状态（稳态）。在稳态，若薄膜两侧之间水蒸气的压力差或相对湿度差一定，并且环境温度也保持恒定时，则湿气将以一定常速透过薄膜。此时，可根据费克第一定律推导出透湿量Q的计算式。

根据费克第一定律，

dm/dt＝－DA（dc/dx）　　　　　　　（2－2－1）

式中：dm/dt为水蒸气透过速率；

　　D为扩散系数；

　　A为膜的面积；

　　dc/dx为膜内水分子的浓度梯度。

　　对于稳态条件，dc/dx为常数B，积分得

B＝－（CH－CL）/L

则有

dm/dt＝－DAB＝DA（CH－CL）/L

积分得到透湿量

∫Q0dm＝[DA（CH－CL）/L]∫t0dt

即

Q＝[DA（CH－CL）/L]t　　　　　　　（2－2－2）

其中：t为测试时间。

图2－2－2给出了透湿量与测试时间的实测曲线。t由图看出：在由t＝0到t＝T的一段时间内，扩散没有达到稳态，Q与t的关系不是直线。定义T为滞后时间。上述定积分的起始时间不应为t＝0，而应为t＝T，即积分结果为

Q＝[DA（CH－CL）/L]（t－T）　　　　　（2－2－3）

由于在实际的包装中所采用的时间t滞后时间T，上式可写成

Q＝D·A[（CH－CL）/L]t

但在测试时，必须考虑滞后时间T。

由于水分子浓度很难测定，所以根据享利定律（C＝Sp），一般用Sp取代C，其中S是水蒸气在薄膜中的溶解度系数，p为水蒸气压，则（2－2－3）式可化为

Q＝DSAt(pH－pL)/L

只要知道D、S、A、t、pH、pL、L等值即可求出透湿量Q值。

三、透湿系数及其计算公式

上面推导出了透湿量的求解公式，但薄膜的溶解系数S、扩散系数D都较难直接测量。所以，我们引进一个新的参数———透湿系数P来代替D和S。

定义P＝D·S，那么

Q＝PAt(pH－pL)/L　或 P＝QL/[At（pH－pL）]　　　　　　（2－2－4）

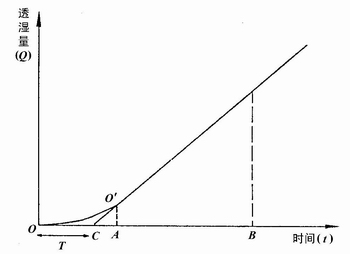
图2－2－2　薄膜透湿量与测试时间的关系图

P的单位是g·cm／（cm2·s·Pa）或g·mm／（m2·d·Pa）。这时Q的单位为g，厚度L的单位为cm或mm，A的单位为cm2或m2，t的单位为s或d，p的单位为Pa。

实际上，透湿系数P真实反映了包装材料的透湿能力，是衡量薄膜透湿性能的一个重要参数。

由于在实际工作中主要以湿度来衡量空气中湿气的含量，而很少采用水蒸气压力，并且测量水蒸气压力比较麻烦，测量相对湿度很容易，所以，为计算上的方便，我们常将p（压力）换算成h（相对湿度）。因h＝p/pθ×100，式中pθ是指θ℃时的饱和水蒸气压，所以透湿量与透湿系数的换算公式可表示成：

Q＝PAt[（hH－hL）pθ×10－2]/L　　　　（2－2－5）

P＝QL/[At（hH－hL）pθ×10－2]　　　　（2－2－6）

由以上公式可以很方便地求得P和Q的值。

在薄膜透湿性能的测定中，一般是在A－B时间内进行测量（见图2－2－2），在薄膜的厚度L、表面积A、两表面之间的湿度差△h即h1－h2为已知的情况下，我们可由直线的斜率直接得知△Q／△t。由

P＝(△Q/△t)·[L/A（hH－hL）pθ×10－2]

求得其薄膜透湿系数P。若做直线的延长线交于横轴C点，则OC即为滞后时间T。由费克第二定律dc/dt＝D(d2c/dx2)，求得

D＝L2/6T　　　　　　（2－2－7）

根据T，代入上式可求出薄膜的透湿扩散系数D的值。同理，也可根据P＝D·S求其溶解度系数S的值。

表2－2－1不同温度下的饱和水蒸气压力值

返回目录页