|
钢桶泄漏流激振动结构响应分析与实验研究
朱志松,郭东军,陈阳阳
摘要:目的为了探究钢桶泄漏产生声发射检测技术的基本原理和实验方法,建立钢桶泄漏仿真模型和实验模型。方法首先介绍钢桶气体泄漏产生声发射信号的机理和流固耦合的基本原理;其次建立钢桶泄漏模型,通过Workbench流固耦合方法模拟流激振动下结构响应特征;然后根据声发射检测原理搭建钢桶泄漏声发射检测实验平台,采集实验数据并分析处理,探讨漏孔直径、内压与钢桶泄漏各特征参数的关联,结合频域分析,得到能够表征钢桶泄漏的特征参数与特征激振频率;最后将得到的泄漏声发射信号特征与仿真结果进行比较。结果钢桶气体泄漏流激振动的激振频段为22~40kHz,峰值频率约为25kHz。结论钢桶泄漏的仿真模拟结果与实验检测得到的结构响应基本一致,钢桶泄漏的仿真与实验研究方法为钢桶气体泄漏在线检测技术的研究提供了依据。
关键词:钢桶泄漏;流固耦合;声发射;结构响应
钢桶从临时储存一般物料演变到当下的运输用包装、销售用包装、工业用包装等领域,从制造到消费,形成了一种流动用工具,成为长期保存内装物料的手段。钢桶生产线已经实现了自动化,由于原材料、生产设施、检测、管理等原因,其出厂质量不理想。泄漏是影响钢桶质量的首要原因,大多泄漏发生在桶身焊缝与桶底卷封处。目前,在钢桶生产线上使用的检漏手段有肥皂水泡沫检测法、压力衰减法等,多数企业使用前者。
钢桶为薄壁结构,钢桶内高压流体从漏孔处向外喷射高速射流对孔壁激励和摩擦,激励漏孔处壁面产生振动,这种振动以应力波形式在桶身传播,即产生了声发射信号。虽然钢桶发生泄漏时产生的声发射信号特征非常复杂,但借助仿真软件对其进行数值模拟,可以对声发射在泄漏孔处产生的影响进行合理的表述和分析。钢桶泄漏时在漏孔处产生射流,射流喷柱是致使钢桶产生声发射信号的主要原因,喷柱的特征决定了声发射源的强度和传播特性,射流喷柱的特征取决于漏孔的大小、形状和钢桶的内压等因素,因此,有必要分析钢桶漏孔在流体激励下结构的响应特征。文中利用有限元流固耦合(FSI)方法分析钢桶泄漏流激振动结构响应,得到其特征频率,并对钢桶泄漏进行实验研究。最后,分析比较仿真与实验的结果。
1 钢桶泄漏数值模拟
1.1 流固耦合基本控制方程
流固耦合分析主要有强耦合和弱耦合等2种方法。强耦合法是将流体与固体控制方程整合并统一、直接求解,流固耦合交界面简化为内部求解域。这种方法虽然清晰明了,但求解时流体与固体的网格尺寸需高度一致,受计算能力的约束,给分析计算带来了很大的不便,工程实际应用少,多用于理论研究。弱耦合的固体域与流体域计算模型需单独建立,流场力利用计算流体力学(CFD)求解模拟,结构响应利用计算结构动力学(CSD)求解分析,然后在交界面上两模型间实现动量的交换,两物理场就完成了耦合过程求解。在求解过程中CFD 和CSD 的求解单独进行,在每个时间步长计算完成后,进行数据交换,从而维护了两模块的独立完整,能够发挥各领域的优越性。根据钢桶泄漏的特征,选用弱耦合进行计算。
在流体作用下,钢桶的结构动力响应运动方程为:
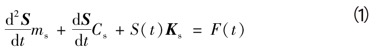
式中:ms为结构质量;Ks为刚度矩阵;Cs为结构阻尼;S为结构振动位移向量;F为钢桶结构外激励力,需要对流体计算才能得到。流体运动需遵循物理守恒定律,包括质量守恒、动量守恒与能量守恒定律。
质量守恒方程即连续性方程,表示单位时间内从控制体流出的流体质量之和应与该时间内由于密度改变而减少的质量相等,由此流体流动连续性方程为:
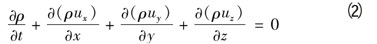
式中:u为流体运动的速度;t为时间;ρ为流体密度。
牛顿第二定律适应动量方程,动量方程也称流体动力学N-S 方程,指流体微单元的动量对时间t的变化率与外界作用在该微单元上各力的合力相等。由此,动量守恒方程表述为:
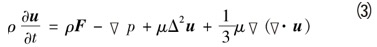
式中:t为时间;u为流体速度向量;为密度;p为流体压强;μ为动力黏度;F为单位质量力向量;∇为哈密顿算子;Δ为拉格朗日算子。
同理,流固耦合问题也应遵循基本的守恒定理。由此,在耦合交界面上需满足方程(4):
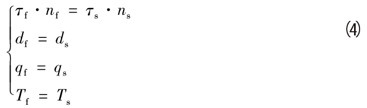
式中:τ为应力;d为位移;q为热流量;T为温度。下标f表示流体,s表示固体。
1.2 流固耦合模型的建立
在Ansys Workbench软件中,利用瞬态动力学Transient Structural模块对钢桶泄漏声发射信号进行数值仿真。模拟分析漏孔直径、内压与钢桶气体泄漏漏孔内壁流激振动响应的特征量的相关性。流场非定常计算采用Fluent软件,控制方程为非定常雷诺平均N-S方程,湍流模型采用标准K-ε模型。
在Transient Structural中建立钢桶结构域有限元模型,材料参数:密度ρ为7800kg/m3,弹性模量E为210GPa,泊松比γ为0.3,结构网格划分为四面体网格。在Fluent中设置流体域各参数,选用理想气体为流动介质,流体网格也采用四面体网格。流体与结构的网格单独划分,网格单元尺寸应满足公式(5)。

式中:L为网格单元尺寸;c为介质中声传播速度;fmax为计算最大频率。
结构域和流体域瞬态分析的时间步长需一致,均设为2.5×10-6s,由于耦合运算量较大,其计算截止时间设为0.0025s,能够满足研究的需要。计算模型为两端开口的圆柱形薄壁钢桶,桶壁厚为1.2mm,钢桶泄漏流体域和结构域模型、网格划分见图1。

图1 钢桶泄漏模型及网格划分
1.3 流固耦合仿真过程
在Fluent中单独求解得到流场各网格点的变量值,如压力、速度等。在Structural中单独计算求出结构场中各节点的应变、位移等量,流场与结构场计算的数据在System Coupling模块上传递交换,且交换是双向的,即压力载荷从流场传递到结构场的结构耦合面上。结构表面的结构位移或应力再传递给流场,从而影响流场分布,然后2个物理场重新开始单独求解,直到耦合交界面上传递的压力载荷和位移数据达到收敛标准时停止迭代,得到这一时间步的最终结果,再进入下一时间步的计算。这样便能计算出流场和结构场的各变量随时间变化的规律。为了得到钢桶泄漏时的流激振动结构响应规律,需要对不同漏孔直径、不同内压下的钢桶数值模拟
1.4 仿真模拟结果与分析
内压为0.18MPa,漏孔直径为0.5mm的钢桶,泄漏桶身结构应力分布情况及漏孔处的放大图见图2。由图2可知,钢桶结构应力响应等值线沿周向分布,远离漏孔处钢桶两端结构应力响应小,越靠近漏孔结构应力响应越明显,在漏孔处达到最大。在漏孔处,结构响应应力轴向分布要明显大于周向,即漏孔处由于喷流作用轴向变形量大。
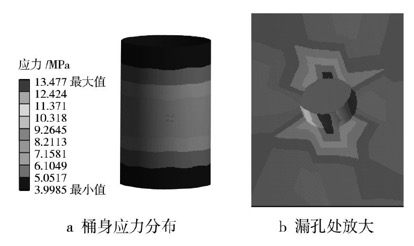
图2 钢桶泄漏结构响应应力分布
为了验证漏孔直径对钢桶泄漏的影响,分析漏孔直径的变化对钢桶泄漏孔处应力强度的影响,漏孔直径D分别设为0.2,0.5,1.0,1.5 mm,内压为0.18 MPa时,泄漏孔径的变化对泄漏孔应力强度的影响见图3。由图3 可以看出,随着钢桶漏孔直径的增加,泄漏孔的应力强度增加缓慢,并没有发生明显变化。由此
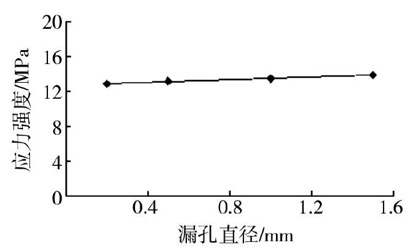
图3 漏孔直径与最大应力强度关系曲线
可见,泄漏孔直径对应力强度的影响非常小。在漏孔壁上取观测点,分析质点随时间变化的振动响应,不同漏孔直径钢桶泄漏流激振动结构响应的应力强度频谱见图4。从图4可以看出,当钢桶漏孔直径变化时,漏孔处的应力幅度、频率以及衰减情况都没有明显变化,这说明泄漏孔径的变化对泄漏孔处质点的应力幅度几乎没有影响,泄漏时的激振频率为23~35 kHz,且在24.8 kHz出现明显的频率尖峰。
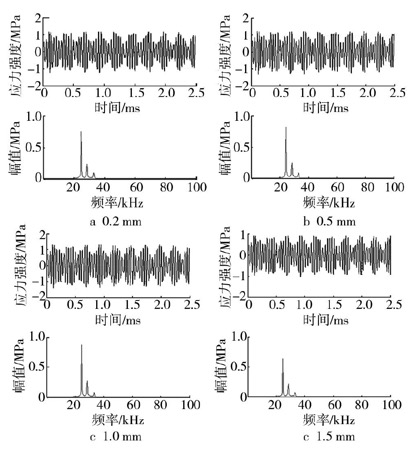
图4 不同漏孔直径的应力强度幅值及频谱图
由于钢桶为薄壁件,因此钢桶内压不宜过大,否则钢桶会发生塑性变形,不能恢复原状。为了验证钢桶内压对泄漏的影响,内压分别设为0.15,0.18,0.21和0.24MPa,分析内压的变化对钢桶泄漏孔处应力强度的影响。漏孔直径为0.5 mm时内压的变化对泄漏孔处应力强度的影响见图5。由图5可以看出,钢桶内压越大,钢桶流激振动结构响应应力强度越大,但随着内压的增大,应力强度并不是成比例的增大,增加的趋势越来越缓慢。
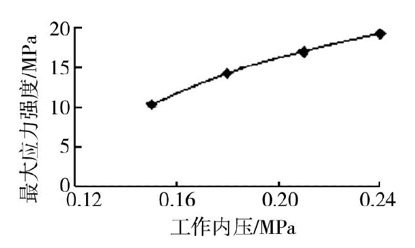
图5 钢桶内压与最大应力强度关系曲线
取漏孔壁上一观测点分析质点随时间变化的振动响应,不同内压下钢桶泄漏流激振动结构响应的应力强度频谱见图6。随着钢桶内压的增加,泄漏孔处质点应力强度逐渐增加,但幅值呈周期性变化,振动频率基本不发生变化。由此可见,对同一直径的钢桶,钢桶内压对泄漏产生的信号频率基本没有影响。不同内压下钢桶泄漏结构响应的激振频率与不同漏孔直径的激振频率基本一致,频率段为22~35kHz,在24.8kHz出现明显的频率峰值。
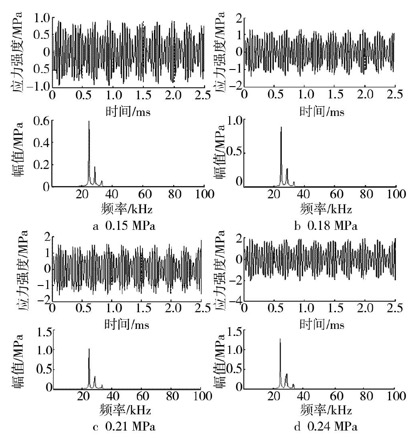
图6 不同内压应力强度幅值及频谱图
2 钢桶泄漏分析
2.1 检测原理
钢桶泄漏缺陷在压力作用下发出一种应力脉冲波,即声发射信号。这种应力脉冲波是一种机械波,传播到材料表面时,声发射传感器接收到这种声发射信号,并将机械信号转换为电信号后,通过与之相连的前置放大器放大送到采集卡上,采集卡再将其转换为数字信号,读取波形数据到计算机。检测系统装置见图7,根据仿真结果,选用中心频率为150 kHz 谐振式高频传感器,北京声华的声发射采集机箱SAEU2S。
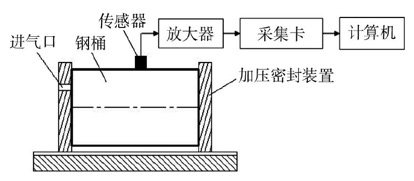
图7 检测系统装置
2.2 结果与分析
分别对不同漏孔直径、不同内压的钢桶(见图7)进行研究。不同漏孔直径和钢桶泄漏信号的最大幅值、激振频段、频率峰值的关系见表1。不同内压和钢桶泄漏信号的最大幅值、激振频段、频率峰值的关系见表2。
表1 不同内压钢桶泄漏实验数据
| 内压/MPa |
最大幅值/V |
激振频段/kHz |
频率峰值/kHz |
0.15 |
0.016 |
22-45,95-115 |
25.6 |
0.18 |
0.025 |
22-45,95-115 |
25.6 |
1.0 |
0.036 |
22-45,95-115 |
25.6 |
由表1和表2可以看出,当内压不同时,声发射信号的幅值有较大的变化。当漏孔直径不同时,其对信号的幅值影响不大。内压与漏孔直径的大小不影响钢桶泄漏时的激振频段与峰值频率的值。
2.2 实验与仿真结果比较
漏孔直径为0.5mm、内压为0.18MPa的钢桶泄漏实验频谱见图8。由图8可知,表征钢桶泄漏的特征激振频率为22~45 kHz和95~115kHz等2个频率段。然而,22~45kHz频率段的信号强度远大于95~115kHz高频段,且峰值频率为25.6 kHz。由前面钢桶泄漏流固耦合结构振动响应分析的频谱分析结果可知,仿真的特征激振频率为20~35kHz,峰值频率为24.8kHz,仿真结果与实验结果得到了较好的吻合,说明利用流固耦合方法对钢桶流激振动声发射信号产生机理仿真研究的可靠性。
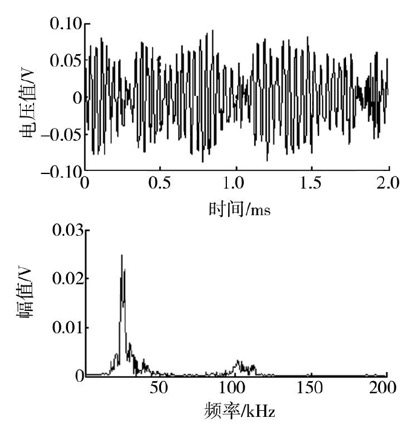
图8 声发射实验信号频谱图
3 结语
采用数值分析与实验方法研究了钢桶气体泄漏流激振动的结构响应,得到如下结论,这些结论对理解钢桶的泄漏机理与利用声发射技术研制钢桶泄漏检测系统至关重要。
1)钢桶存在泄漏孔时,高速流体对漏孔孔壁的激励产生振动,这种振动是产生声发射信号的主要原因。射流喷柱是钢桶产生泄漏声发射信号的主要原因,喷柱的特征决定了声发射源的强度和传播特性。
2)建立了钢桶泄漏的流固耦合仿真模型,借助有限元分析软件进行了分析:钢桶泄漏结构响应等值线沿周向分布,漏孔处结构响应最大,远离漏孔处钢桶两端结构应力响应越小。漏孔处的结构响应轴向应力分布要明显大于周向分布。
3)采用控制变量法,分别对不同漏孔直径与内压的钢桶泄漏时流固耦合流激振动结构的响应进行了数值分析。随着钢桶漏孔直径的增大,无论是漏孔处的应力幅度、激振频率段和频率峰值都没有明显变化。随着钢桶内压的增加,泄漏孔处应力强度幅值明显逐渐增加,但振动频率段基本不发生变化,即流激作用下泄漏孔处质点激振频率和峰值频率不随漏孔直径和内压的变化而变化,24.8 kHz 为其激振峰值频率。
4)根据仿真结果对实验器材选型、实验,对不同孔径与内压的钢桶检测可知,钢桶实验结果与数值分析结果吻合较好。根据数值模拟结果推断钢桶检测的可行性,利用实验结果验证了仿真数据的可靠性。数值分析与实验研究为后期钢桶检测系统的开发提供了理论依据和实验方案。
参考文献:
[1] 杨文亮.论钢桶包装业发展趋势[J].中国包装,2001(2):45—49.
[2] 陆楠,李居峰,卢鲜亮.基于ANSYS 的钢桶焊缝处理分析[J].机械制造,2012(3):57—59.
[3] KAEWWAEWNOI W,PRATEEPASEN A. Investigation of the Relationship between Internal Fluid Leakage through a Valve and the Acoustic Emission Generated from the Leakage [J]. Measurement,2010,43:274—282.
[4] 李兵,谢里阳,郭星辉等.流体对薄壁圆柱管振动频率的影响[J].振动与冲击,2010,29(7):193—195.
[5] 刘贵杰,徐萌,王欣等.基于HHT的管道阀门内漏声发射检测研究[J].振动与冲击,2012,31(23):62—66.
[6] 李宏宇,李建昌,孙越等.平口喷嘴的真空射流雾化模拟分析[J].真空科学与技术学报,2013,33(3):284—288.
[7] 姬贺炯,白长青,韩省亮.输流管道动力有限元建模及实验研究[J].应用力学学报,2013,30(3):422—427.
[8] 李艳华,柳贡民,马俊.考虑流固耦合的典型管段结构振动特性分析[J].振动与冲击,2010,29(6):50—53.
[9] KENNEDY,EBERHART R C.Particle Swarm Optimization [C]// Proceedings of the 1995 IEEE International Conference on Neural Networks.Australia,1995:1942—1948.
[10] DHANDOLE S,MODAK S V.On Improving Weekly Coupled Cavity Models for Vibro-acoustic Predictions and Design[J]. Applied Acoustics,2010,71:876—884.
[11] 张智勇,沈荣瀛.充液直管管系中的固-液耦合振动响应分析[J]. 振动工程学报,2000,13(3):455—461.
[12] 张瑞琴,翁建生.基于流固耦合的叶片颤振分析[J].计算机仿真,2011,28(3):48—51.
[13] 包日东,金志浩,闻邦椿.分析一般支承输流管道的非线性动力学特性[J].振动与冲击,2008,27(7):87—90.
[14] SEMLER C,LI G X,PAIDOUSSIS M P. The Non-linear Equations of Motion of Pipes Conveying Fluid[J]. Journal of Sound and Vibration,1994,169(5):577—599.
[15] SREEJITH B,JAYARAJ K,GANESAN N. Finite Element Analysis of Fluid-structure Interaction in Pipeline Systems [J]. Nuclear Engineering and Design,2004,227(3):313—322.
|

